Seek and You Shall Scan Part I: When the Optimizer Doesn't Optimize

Index Seek and Index (or Table) Scan are two of the most common operators that you see in query execution plans. A common misconception is that a scan is bad and a seek is good. The reality is that each is optimal under different circumstances. In some cases the optimizer chooses between the two based on which is indeed more optimal in the given situation. In those cases, other than appreciating the optimizer’s ability to come up with the truly optimal plan, there’s nothing special that we need to do. However, what’s interesting to us as people who tune queries is to identify cases, or patterns, in which the optimizer doesn’t make the optimal choice and act to fix them.

This article starts by demonstrating language elements for which the optimizer is able to choose the optimal strategy based on data characteristics and index availability. Specifically, I’ll demonstrate solutions to semi and anti-semi joins using the EXISTS predicate. The article then continues by showing language elements that are optimized with more limited possible alternatives, and then you need to make sure that you use the solution that gives you the optimal plan. Specifically, I’ll demonstrate solutions to the grouped MIN/MAX and top N per group problems.

Sample Data

Use the code in Listing 1 to create the sample data for this article.

Listing 1: Code to create sample dataSET NOCOUNT ON;USE tempdb;GOIF OBJECT_ID(N'dbo.Orders'   , N'U' ) IS NOT NULL DROP TABLE dbo.Orders;IF OBJECT_ID(N'dbo.Customers', N'U' ) IS NOT NULL DROP TABLE dbo.Customers;IF OBJECT_ID(N'dbo.Employees', N'U' ) IS NOT NULL DROP TABLE dbo.Employees;IF OBJECT_ID(N'dbo.GetNums'  , N'IF') IS NOT NULL DROP FUNCTION dbo.GetNums;GO-- Definition of GetNums functionCREATE FUNCTION dbo.GetNums(@low AS BIGINT, @high AS BIGINT) RETURNS TABLEASRETURN  WITH    L0   AS (SELECT c FROM (VALUES(1),(1)) AS D(c)),    L1   AS (SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B),    L2   AS (SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B),    L3   AS (SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B),    L4   AS (SELECT 1 AS c FROM L3 AS A CROSS JOIN L3 AS B),    L5   AS (SELECT 1 AS c FROM L4 AS A CROSS JOIN L4 AS B),    Nums AS (SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum        FROM L5)  SELECT TOP(@high - @low + 1) @low + rownum - 1 AS n  FROM Nums  ORDER BY rownum;GO-- Data distribution settings for ordersDECLARE  @numorders   AS INT      =   1000000,  @numcusts    AS INT      =     20000,  @numemps     AS INT      =       100,  @numshippers AS INT      =     5,  @numyears    AS INT      =     4,  @startdate   AS DATE     = '20110101';-- Creating and populating the Customers tableCREATE TABLE dbo.Customers(  custid   CHAR(11)     NOT NULL,  custname NVARCHAR(50) NOT NULL);INSERT INTO dbo.Customers(custid, custname)  SELECT    'C' + RIGHT('000000000' + CAST(T.n * @numcusts + N.n AS VARCHAR(10)), 10) AS custid,    N'Cust_' + CAST(N.n AS VARCHAR(10)) AS custname  FROM dbo.GetNums(1, @numcusts) AS N    CROSS JOIN ( VALUES(0),(1) ) AS T(n);ALTER TABLE dbo.Customers ADD  CONSTRAINT PK_Customers PRIMARY KEY(custid);-- Creating and populating the Employees tableCREATE TABLE dbo.Employees(  empid     INT      NOT NULL,  firstname NVARCHAR(25) NOT NULL,  lastname  NVARCHAR(25) NOT NULL);INSERT INTO dbo.Employees(empid, firstname, lastname)  SELECT T.n * @numemps + N.n AS empid,    N'Fname_' + CAST(N.n AS NVARCHAR(10)) AS firstname,    N'Lname_' + CAST(N.n AS NVARCHAR(10)) AS lastname  FROM dbo.GetNums(1, @numemps) AS N    CROSS JOIN ( VALUES(0),(1) ) AS T(n);ALTER TABLE dbo.Employees ADD  CONSTRAINT PK_Employees PRIMARY KEY(empid);-- Creating and populating the Orders tableCREATE TABLE dbo.Orders(  orderid   INT    NOT NULL,  custid    CHAR(11)   NOT NULL,  empid     INT    NOT NULL,  shipperid VARCHAR(5) NOT NULL,  orderdate DATE       NOT NULL,  filler    CHAR(160)  NOT NULL DEFAULT('a'));INSERT INTO dbo.Orders(orderid, custid, empid, shipperid, orderdate)  SELECT n AS orderid,    'C' + RIGHT('000000000'        + CAST(        1 + ABS(CHECKSUM(NEWID())) % @numcusts        AS VARCHAR(10)), 10) AS custid,    1 + ABS(CHECKSUM(NEWID())) % @numemps AS empid,    CHAR(ASCII('A') - 2       + 2 * (1 + ABS(CHECKSUM(NEWID())) % @numshippers)) AS shipperid,  DATEADD(day, n / (@numorders / (@numyears * 365.25))           -- late arrival with earlier date         - CASE WHEN n % 10 = 0           THEN 1 + ABS(CHECKSUM(NEWID())) % 30           ELSE 0          END, @startdate)     AS orderdate  FROM dbo.GetNums(1, @numorders)  ORDER BY CHECKSUM(NEWID())OPTION(MAXDOP 1);ALTER TABLE dbo.Orders ADD  CONSTRAINT PK_Orders PRIMARY KEY(orderid);CREATE INDEX idx_eid_oid_i_od_cid  ON dbo.Orders(empid, orderid DESC)    INCLUDE(orderdate, custid);CREATE INDEX idx_cid_oid_i_od_eid  ON dbo.Orders(custid, orderid DESC)  INCLUDE(orderdate, empid);GO

The code creates a table called Orders with 1,000,000 orders; a table called Employees with 200 employees, of which 100 handled orders; and a table called Customers with 40,000 customers, of which 20,000 placed orders. The code also creates a few indexes on the Orders table to illustrate optimization choices.

Scan vs. Seek

There are many examples for tasks that involve applying some logic per group that requires examination of one or just a few rows per group. Among those are:

The solutions to the above tasks can greatly benefit from what you can think of as a POC index on the large table (Orders, in our case). The POC acronym represents the elements involved in the query and that should appear in the index definition. Those are Partitioning, Ordering and Coverage. For example, for the task “return the order (orderid, orderdate, empid, custid) with the maximum order ID per employee” P = empid, O = orderid DESC, and C = orderdate, custid. The P and O elements should make the index key list, and the C element should make the INCLUDE list. Indeed, one of the indexes that Listing 1 creates to demonstrate the optimization of such a task with a POC index is the following:

CREATE INDEX idx_eid_oid_i_od_cid  ON dbo.Orders(empid, orderid DESC)    INCLUDE(orderdate, custid);

What’s interesting is that, depending on the density of the group/partitioning element, different optimization strategies are optimal.

If the partitioning element is dense (small number of distinct values, each appearing many times), the best strategy is to use a seek in the index per distinct value. For example, the empid column in the Orders table has high density (100 distinct employee ID values). So the optimal strategy to return the order with the maximum order ID per employee is to scan the Employees table, and to apply in a loop a seek in the POC index on Orders per employee. With 200 employees in the Employees table you will get 200 seeks, which should amount to a few hundred reads in total. That’s compared to a few thousand reads that a full scan of the POC index would cost you.

Conversely, the custid column has low density in the Orders table (20000 distinct customer ID values). With 40,000 customers in the Customers table, the strategy with the seeks will cost you over a hundred thousand reads, whereas a scan would cost you just a few thousand.

In short, for tasks that involve doing work per group that requires visiting a small number of rows per group, for low density a scan is optimal and for high density seeks are optimal. Now let’s examine the aforementioned examples and see when the optimizer comes up with the optimal strategy by itself and when it needs a bit of help.

Semi/Anti-Semi Joins

When the optimizer optimizes queries with the EXISTS predicate (as well as some other methods) to handle semi and anti-semi joins, it is certainly able to explore candidate plans including one with a scan and one with a loop of seeks against the index on the larger table. In fact, it goes well beyond just a scan vs a loop of seeks. It has all three join algorithms available to it (nested loops, merge and hash). But my point is that potentially the optimizer is able to choose the optimal strategy based on the data characteristics, among other things.

As an example, consider the following two semi join queries:

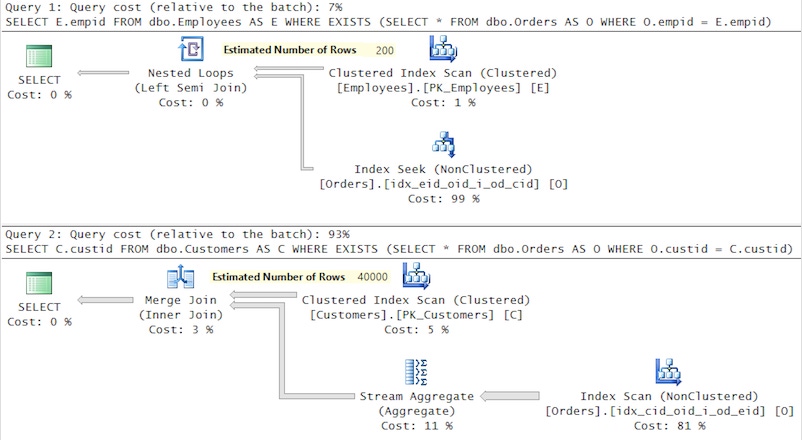
-- High density – seeks, logical reads 4 + 670SELECT E.empidFROM dbo.Employees AS EWHERE EXISTS  (SELECT *   FROM dbo.Orders AS O   WHERE O.empid = E.empid);-- Low density – scan, logical reads 110 + 3481SELECT C.custidFROM dbo.Customers AS CWHERE EXISTS  (SELECT *   FROM dbo.Orders AS O   WHERE O.custid = C.custid);

The plans for these two queries is shown in Figure 1.

[Figure 01 - Semi Joins]

The plan for the first query with the high density of the partitioning element performs a loop of seeks against the index on Orders. The plan for the second query with the low density of the partitioning element performs a scan against the index on Orders.

You will see a similar dynamic choice of the optimizer with anti-semi joins, such as in the following two queries:

-- High density – seeks, logical reads 4 + 670SELECT E.empidFROM dbo.Employees AS EWHERE NOT EXISTS  (SELECT *   FROM dbo.Orders AS O   WHERE O.empid = E.empid);-- Low density – scan, logical reads 218 + 3481SELECT C.custidFROM dbo.Customers AS CWHERE NOT EXISTS  (SELECT *   FROM dbo.Orders AS O   WHERE O.custid = C.custid);

The plans for these queries is shown in Figure 2.

[Figure 02 - Anti-Semi Joins]

Again, in the case with low density the plan uses a scan, and in the case with high density it uses seeks.

Grouped MIN/MAX

A grouped MIN/MAX task is simply a case where you’re after the minimum or maximum value per group. The most natural way to address such a task is with a simple grouped query. Having a PO index in place (C is irrelevant here), theoretically, the optimizer could have evaluated the density of the group column and chosen a scan vs. a loop of seeks strategy accordingly. However, currently there’s no logic in the optimizer to do a loop of seeks for a grouped query. So irrespective of the density, the plan will scan the index. This is good if you have low density (for example, if you group by custid), but bad if you have high density (for example, if you group by empid).

To demonstrate a suboptimal case with high density, consider the following query:

-- logical reads 3474SELECT empid, MAX(orderid) AS maxoidFROM dbo.OrdersGROUP BY empid;

The plan for this query appears as the first plan in Figure 3.

If you want to get a plan that applies a seek per employee, you need to rewrite your solution. One way to achieve this is to use the CROSS APPLY operator, like so:

-- logical reads 4 + 670SELECT E.empid, O.orderidFROM dbo.Employees AS E  CROSS APPLY (SELECT TOP (1) O.orderid       FROM dbo.Orders AS O       WHERE O.empid = E.empid) AS O;

The plan for this query is shown as the second plan in Figure 3.

[Figure 03 - Grouped MAX]

As you can see, that’s the desired plan. If you’re wondering why use the CROSS APPLY operator and not just a scalar correlated subquery, remember that CROSS APPLY will eliminate left rows that have no matches, which is the desired behavior in this case.

Top N Per Group

The top N per group task (for example, last order per employee/customer) is another one of those tasks for which the typical solutions get a fairly static plan shape; that’s at least the case in terms of a scan vs a loop of seeks. The two typical solutions are:

1. Compute row numbers and filter the rows where the row number is equal to 1. This solution always gets a scan.

2. Query the table representing the groups/partitions, and use the CROSS APPLY operator to apply a TOP (1) query against the larger table. This solution gets a loop of seeks.

So, to return the last order per customer (low density), you should use the solution with the ROW_NUMBER function. To return the last order per employee (high density), you should use the solution with the CROSS APPLY operator. Here are both examples:

-- To get a scan use ROW_NUMBER (low density), logical reads 3481WITH C AS(  SELECT ROW_NUMBER() OVER(PARTITION BY custid ORDER BY orderid DESC) AS n,    *  FROM dbo.Orders)SELECT custid, orderdate, orderid, empidFROM CWHERE n <= 1;-- To get seeks use APPLY (high density), logical reads 4 + 670SELECT E.empid, O.orderdate, O.orderid, O.custidFROM dbo.Employees AS E  CROSS APPLY (SELECT TOP (1) *       FROM dbo.Orders AS O       WHERE O.empid = E.empid       ORDER BY orderid DESC) AS O;

The plans for these queries are shown in Figure 4.

[Figure 04 - Top N Per Group]

Proxy CROSS APPLY

A curious case related to the last example was introduced by SQL Server MVP Erland Sommarskog in a private group. An interesting discussion developed around it with contributions by Hugo Kornelis, Paul White and others. Suppose that you need to add to the last query’s SELECT list columns from the Orders table that are not covered by the index. For example, the following query adds a column called filler to the SELECT list:

-- logical reads 2445833SELECT E.empid, O.orderdate, O.orderid, O.custid, O.fillerFROM dbo.Employees AS E  CROSS APPLY (SELECT TOP (1) *       FROM dbo.Orders AS O       WHERE O.empid = E.empid       ORDER BY orderid DESC) AS O;

This small change seems to have severe implications on the performance of the query. Without the extra column, the query performed only a few hundred reads and finished in 77 milliseconds on my system. With the extra column, the query performs about 2.5 million reads and takes about 8 seconds to complete. You would think that the optimal plan for the new query should perform the following per employee:

But if you examine the plan for the query in Figure 5, you see that the optimizer chose a different strategy.

[Figure 05 - Top N Per Group - noncovering index – suboptimal]

Instead of doing a double-seek approach (seek in nonclustered, then lookup in clustered) per employee, the plan does (per employee) an ordered scan of the clustered index that is capped by a Top operator as soon as a row is found. Remember that the clustered index key is the orderid column. So as soon as the first row with the outer empid value is found, the scan stops, and the order elements from that row are returned. This strategy might seem strange, but for better or worse (in our case for worse), based on the existing optimization and cardinality estimation model, there’s some logic behind this approach.

The optimization model uses assumption known as containment and inclusion. Containment assumes that if you’re looking for something, it actually exists. In an equijoin case the assumption is that distinct join column values in one side do exist in the other side. The inclusion assumption is similar but for an equality filter predicate with a constant--that the filtered value actually exists. Observe the residual predicate in the Clustered Index Scan operator: O.empid = E.empid. Based on the model’s assumptions, if every employee ID that the scan is looking for indeed exists, statistically, one in every hundred rows will be a match (the density of Orders.empid is 0.01). So, statistically, it should take only a couple of page reads before a matching row is found. If the model’s assumptions were correct, this strategy would have been better than the double-seek strategy. However, the model’s assumptions fail in our case since we have 200 employees in the Employees table, with 100 of them who don’t have matching orders. So 100 times, the scan is done to completion. Consequentially, the performance of this solution is very poor.

There are a number of possible fixes here. If extending the index to include the missing columns (filler in our case) is an option, that’s best. You’ll get a plan similar to the second plan in Figure 4. If that’s not an option, another solution is to specify an index hint against the Orders table: WITH (INDEX(idx_eid_oid_i_od_cid)). You’ll get the double-seek strategy. If you prefer not to use a hint, another option is to use what I call a proxy CROSS APPLY approach. With this approach you use two CROSS APPLY operators. The intermediate one is only there to compute the qualifying order ID for the current employee with a TOP (1) query, but doesn’t return any of its own elements to the outer query. It invokes an inner CROSS APPLY operator and passes to the inner query the qualifying order ID, and then the inner query returns the respective row from the Orders table. The proxy CROSS APPLY query passes the row from the inner CROSS APPLY query back to the outer query, and the outer query in turn returns the desired elements of the order. If this explanation doesn’t make much sense, look at the solution query and read the explanation again:

-- Proxy CROSS APPLY, logical reads 4 + 922SELECT E.empid, P.orderdate, P.orderid, P.custid, P.fillerFROM dbo.Employees AS E  CROSS APPLY (SELECT TOP (1) O.*       FROM dbo.Orders AS P         CROSS APPLY           (SELECT O.*            FROM dbo.Orders AS O            WHERE O.orderid = P.orderid) AS O       WHERE P.empid = E.empid       ORDER BY orderid DESC) AS P;

The plan for this query is shown in Figure 6.

[Figure 06 - Top N Per Group - noncovering index – optimal]

As you can see, this time the plan applies the double-seek strategy instead of a scan. It applies only a few hundred reads and finishes in 90 milliseconds.

When you’re done, run the following code for cleanup:

USE tempdb;IF OBJECT_ID(N'dbo.Orders'   , N'U' ) IS NOT NULL DROP TABLE dbo.Orders;IF OBJECT_ID(N'dbo.Customers', N'U' ) IS NOT NULL DROP TABLE dbo.Customers;IF OBJECT_ID(N'dbo.Employees', N'U' ) IS NOT NULL DROP TABLE dbo.Employees;IF OBJECT_ID(N'dbo.GetNums'  , N'IF') IS NOT NULL DROP FUNCTION dbo.GetNums;

Conclusion

To seek or to scan, that is the question. This article shows that in some cases the optimizer figures out the optimal choice by itself, for example, when using the EXISTS predicate to handle semi and anti-semi joins. However, in some cases, like with a grouped MIN/MAX aggregate and top N per group problems, you need to write a specific query solution to get the plan shape that is optimal. In another column I’ll describe the ascending key problem, which demonstrates how, due to inaccurate cardinality estimates, the optimizer might end up choosing a suboptimal strategy, and what you can do to address the problem.